Mat. dan Ilmu Alamiah Dasar minggu ke-12

PRODUK KARTESIUS DAN RELASI

 

Himpunan semua pasangan berurutan (a,b) dengan a A dan b B disebut himpunan perkalian A dan B atau produk kartesius A dan B ditulis dengan notasi     A x B dan didefinisikan sbb ; A x B = {(a,b) : a A, b B}
Cece Kustiawan, FPMIPA, UPI
Contoh
Jika A = {1, 2, 3} dan B = {a, b}, maka          A x B = {(1,a), (2,a), (3,a), (1,b), (2,b), (3,b)}    dan B x A = {(a,1), (a,2), (a,3), (b,1), (b,2), (b,3)}

RELASI MATRIKS

Misalkan R adalah relasi dari A = {a₁, a₂, . . .,a_m} dan B = {b₁, b₂, . . .,b_n}, relasi R dapat disajikan dengan matriks M = [m_ij]

Yang dalam hal ini :

Dengan kata lain, elemen matriks pada posisi (i,j) bernilai 1 jika a_i dihubungkan dengan b_j dan bernilai 0 jika a_i tidak dihubungkan dengan b_j.

Relasi R pada table 1 dapat dinyatakan dengan matriks :

yang dalam hal ini, a₁ = Amir, a₂ = Budi, a₃ = Cecep, dan b₁ = INF0221

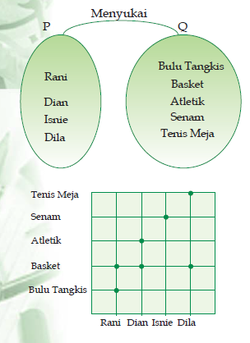
Diagram Panah

Anggota-anggota himpunan P berelasi dengan anggota himpunan Q dengan relasi “menyukai”. Hal tersebut ditunjukkan dengan arah panah. Oleh karena itu, diagramnya disebut diagram panah.

RELASI INVERS

Misalkan R adalah relasi dari himpunan A ke himpunan B. Invers dari R yang dinyatakan dengan R-1 adalah relasi dari B ke A yang mengandung semua pasangan terurut yang bila dipertukarkan masih termasuk dalam R. Ditulis dalam notasi himpunan sbb ; R-1 = {(b,a) : (a,b) R}
Cece Kustiawan, FPMIPA, UPI
Contoh Relasi Invers
Misalkan A = {1, 2} dan B = {a, b}, maka R = {(1,a), (1,b), (2,a), (2,b)} merupakan suatu relasi dari A ke B. Tentukan relasi invers dari R ! Relasi invers dari R adalah ; R-1 = {(a,1), (b,1), (a,2), (b,2)}

KOMPOSISI RELASI

Komposisi relasi seperti halnya komposisi fungsi jadi seperti  kombinasi hanya beda macam operasinya.

Misal R adalah relasi dari himpunan A ke himpunan B, dan S adalah relasi dari himpunan B ke himpunan C. komposisi R dan S dinotasikan dengan  R₀S adalah relasi dari A ke C yang didefinisikan oleh

          R₀S = {(a,c)|aЄA, c Є C, dan untuk beberapa bЄB, (a,b)ЄR dan (b,c)ЄS}

Contoh

Misalkan R = {( 1,2),(1,6),(2,4),(3,4),(3,6),(3,8)} adalah relasi dari A={1,2,3} dan B={2,4,6,8} ,dan

 S={( 2,u),(4,s),(4,t),(6,t),(8,u)} adalah relasi dari B ke C={s,t,u}. Tentukan komposisi relasi R dan S yaitu R₀S

Jawab

R₀S = {(1,u),(1,t),(2,s),(2,t),(3,s),(3,t),(3,u)}

Jika relasi R₁ dan R₂ masing-masing dinyatakan dalam matriks M_R1 dan M_R2, maka matriks yang menyatakan komposisi dari relasi tersebut adalah

                                                                                        M_R1oR2= M_R1 . M_R2

operator “ ₀ “ sama seperti pada perkalian matrik, tetapi mengganti tanda kali dg L, sedangkan jumlah dengan V

Dalam hal ini ingat operasi pada aljabar bool yaitu tanda atau(V)  seperti jumlah sedang kan tanda dan(L) seperti kali

1. Refleksif

Relasi R pada himpunan A disebut refleksif,  jika (a,a)ЄR untuk setiap aЄA.

Contoh

Relasi R didefinisikan pada himpunan A dimana  A={1,2,3,4}

a) Diketahui ,  R={(1,1), (1,3),(2,1), (2,2), (3,3), (4,2), (4,3), (4,4)}

b) Diketahui , R={(1,1),  (2,2), (2,3), (4,2), (4,3), (4,4)}.

Tentukan apakah R refleksif ?

Jawab

a) bersifat refleksif karena  (a,a) ada dalam R yaitu (1,1), (2,2), (3,3), dan (4,4)

b) tidak refleksif karena ada (a,a) tidak ada dalam R yaitu (3,3).

Dilihat dari cara penulisan relasi, relasi yang bersifat refleksif mempunyai matriks  denganbentuk semua bernilai 1 pada diagonal utamanya ,  sedangkan graf berarah adanya gelang pada setiap simpulnya.

2. Simetris (setangkup)

Sebaliknya dikatakan tidak simetris.

Contoh

Relasi R didefinisikan pada himpunan A dimana  A={1,2,3,4}

a) Diketahui ,  R={(1,1), (1,2),(2,1), (2,2), (2,4), (4,2), (4,4)}

b) Diketahui , R={(1,1),  (2,3), (4,2), (4,3), (4,4)}.

Tentukan apakah R simetris ?

Jawab

a) simetris karena jika (a,b)ЄR, ada juga  (b,a)ЄR yaitu (1,2) , (2,1) ЄR, begitu juga (2,4) , (4,2)ЄR

b) tidak simetris karena (2,3)ЄR tetapi (3,2) tidak dalam R

Dilihat cara penulisan relasi, relasi bersifat simetris mempunyai matriks yang elemen-elemen dibawah diagonal utama merupakan pencerminan dari elemen-elemen diatas diagonal utama, atau m_ij = m_ji umtuk i= 1,2,.......n. sedangkan graf berarahnya mempunyai ciri : jika ada busur a ke b, maka ada juga busur dari b ke a

3. Transitif (penghantar)

Relasi R pada himpunan A disebut  transitif (penghantaf), untuk a, b, c Є A, jika (a,b)ЄR dan (b,c)ЄR,maka harus ada (a,c)ЄR.

Contoh

Misal A={1,2,3,4}, dan relasi R pada A

a) diketahui R= {(2,1), (3,1),(3,2), (4,1), (4,2), (4,3)}

b) Diketahui , R={(1,1),  (2,3),  (2,4), (4,2)}.

Tentukan apakah R refleksif ?

Jawab

a) transitif karena memenuhi syarat untuk, a,b,c ЄA, jika ada (a,b)ЄR dan (b,c)ЄR,maka terlihat ada (a,c)ЄR.

b) tidak bersifat transitif karena tidak memenuhi syarat untuk, a,b,c ЄA, jika ada (a,b)ЄR dan (b,c)ЄR,tidak terlihat ada (a,c)ЄR. Dalam hal ini ada (2,4), dan(4,2) tetapi (2,2)ÏR

NAMA : PRISTA DICA KURNIA

NPM : 16513934

KELAS : 1PA10